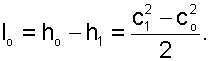
(4.1)
Сопловой канал – устройство для увеличения кинетической энергии потока. В сопловых каналах скорости истечения газа или жидкости велики, а длина канала мала. В таких устройствах теплообмен с окружающей средой практически отсутствует, а процесс истечения считается адиабатным (q=0). Технической работы в сопловых каналах не производится lТ=0. Первый закон термодинамики для обратимого адиабатного процесса истечения вещества в сопловом канале будет иметь вид
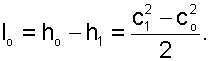 |
(4.1) |
В выражении 4.1 индексом о будем обозначать параметры и скорость на входе в сопло, а индексом 1 – на выходе из сопла (рис.4.1).
Для упрощения анализа процесса истечения через сопловой канал в качестве рабочего тела первоначально примем идеальный газ с постоянными теплоемкостями сР, сV и коэффициентом Пуассона к.
Из выражения 4.1 можно получить расчетную формулу для скорости на выходе из соплового канала:
(4.2) |
При истечении через сопло идеального газа, состояние которого изменяется по адиабате с показателем к=const, т.е.
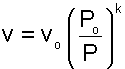 |
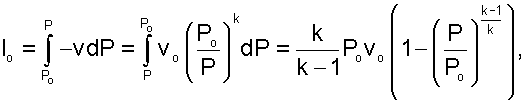 |
(4.3) |
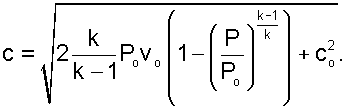 |
(4.4) |
Для упрощения анализа процесса истечения газа через сопло примем входную скорость равной нулю (сО=0). Начальные параметры газа на входе в сопло будем считать постоянными. Возьмем произвольное сечение соплового канала и проведем анализ процесса истечения при изменении давления в этом сечении от Р=РО до Р=0. Согласно выражения 4.4 скорость истечения в этом канале будет рассчитываться по формуле
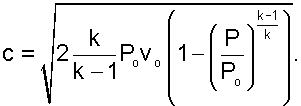 |
(4.5) |
Величину Р/РО, обозначим как e=Р/РО и назовем ее степенью изменения давления. Эта величина является определяющей в выражении 4.5, поскольку все остальные величины постоянные. Воспользуемся уравнением неразрывности потока для дальнейшего анализа в виде
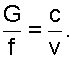 |
(4.6) |
Величина G/f – удельный массовый секундный расход газа через единицу площади поперечного сечения сопла. Эта величина позволяет провести анализ процесса истечения газа через сопло. Выразив удельный объём газа в данном сечении соплового канала из уравнения адиабаты:
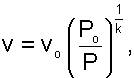 |
(4.7) |
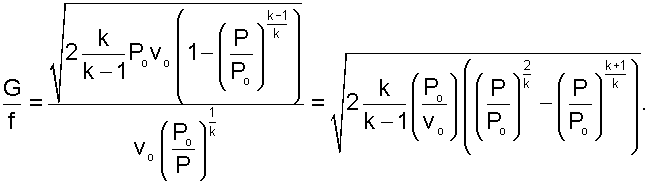 |
(4.8) |
Из выражения (4.8) следует, что при Р=РО и Р=0, удельный расход равняется нулю. В первом случае (Р=РО) работа изменения давления в потоке и скорость равны нулю, поэтому нет истечения и расход равен нулю; во втором случае (Р=0)удельный объём газа бесконечно велик (истечение в вакуум), а скорость истечения имеет конечное максимальное значение, соответствующее выражению:
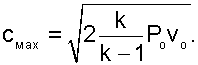 |
(4.9) |
Уравнение (4.8) выражает функциональную зависимость между удельным расходом газа и отношением Р/РО, которое обозначено через e. Представим зависимость G/f = F(e) графически на рис.4.2.
Эта функция непрерывна и положительна на интервале 0<e<1, при e=0 и e=1 она равна нулю, следовательно, на данном интервале она имеет максимум.
Значение аргумента e при максимуме данной функции назовём критическим отношением давлений – eКР. Оно определяется как первая производная функции (4.8), приравненной к нулю. В результате такого дифференцирования получаем:
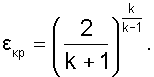 |
(4.10) |
Величина eКР зависит от показателя адиабаты, следовательно, для идеального газа с постоянными изобарными и изохорными теплоемкостями она постоянная (двухатомный газ к=1,4, eКР = 0,528). Для реального газа она зависит от параметров состояния (перегретый водяной пар к ≈ 1,3, eКР ≈ 0,546; для сухого насыщенного пара к ≈ 1,135, eКР ≈ 0,577).
Подставив eкр в выражение скорости истечения (4.5), получим расчетное выражение для критической скорости
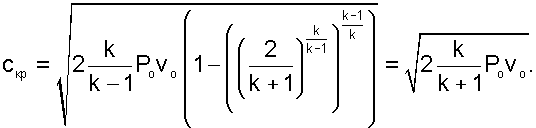 |
(4.11) |
Итак, при истечении газа через сопло с понижением давления от РО до РКР удельный расход газа G/f сначала возрастает, при РКР достигает максимума, а при дальнейшем понижении давления – уменьшается. Следовательно, при постоянстве массового расхода газа G=const, по всей длине соплового канала площадь сечения в диапазоне давлений от РО до РКР должна уменьшаться, а при давлениях ниже РКР площадь его сечения должна увеличиваться.
Для объяснения такой закономерности изменения площади поперечного сечения канала проведём математический анализ уравнения неразрывности Gv = fc. Продифференцировав его при G = const, получим соотношение
Поделив последнее на Gv=fc, получим зависимость изменения относительного объема газа при истечении его в сопловом канале
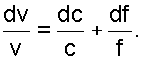 |
(4.12) |
Из 4.12 выразим величину изменения относительной площади поперечного сечения соплового канала:
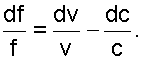 |
(4.13) |
Из уравнения (4.13) следует, что канал суживается (df/f < 0) в случае большего относительного возрастания скорости газа по отношению к относительному возрастанию его удельного объёма (dc/c > dv/v). В случае, когда преобладает рост относительного удельного объёма газа по сравнению с относительным ростом его скорости (dv/v > dc/c) – канал расширяется (df/f > 0). При РКР меняется знак df, т.е. профиль канала переходит из суживающегося в расширяющийся. В самом узком сечении канала устанавливаются параметры, называющиеся критическими (РКР, vКР, tКР, cКР).
Для установления зависимости между критической скоростью и параметрами газа в критическом сечении сопла выразим dv/v из уравнения адиабаты Рvk = const, продифференцировав его и поделив на постоянную РvК получим,
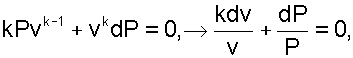 |
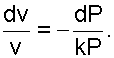 |
(4.14) |
Величину dc/c выразим из уравнения работы изменения давления в потоке для обратимого процесса в сопловом канале
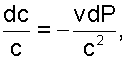 |
(4.15) |
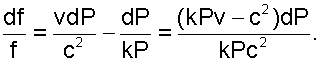 |
(4.16) |
Поскольку при истечении через сопловый канал давление уменьшается (dР < 0), то канал будет суживаться (df < 0) при ![]() , и наоборот канал расширяется (df>0) при
, и наоборот канал расширяется (df>0) при ![]() . В самом узком сечении канала (df = 0) устанавливается критическая скорость, определяемая выражением:
. В самом узком сечении канала (df = 0) устанавливается критическая скорость, определяемая выражением:
(4.17) |
Из физики известно, что выражение (4.17) определяет скорость распространения звука в газовой среде при данных термических параметрах, обозначим её буквой α. При адиабатном истечении газа температура газа уменьшается по длине канала в направлении движения потока, следовательно, уменьшается и его скорость звука, а скорость истечения газа растёт. В суживающейся части сопла с<α. В минимальном сечении канала скорость звука газа равна его скорости истечения сКР=αКР. В расширяющейся части сопла скорость истечения газа больше скорости звука (с>α).
На рис. 4.3 представлена графическая зависимость изменения v, c, α, f при адиабатном расширении идеального газа в сопловом канале от неизменных начальных параметров, нулевой начальной скорости и изменении давления за соплом от Р=РО до Р=0.
При начальном давлении РО и удельном объёме газа vО начальная скорость его cО равна нулю (так приняли), при этом площадь сечения канала бесконечно велика (fО=GvО/0=∞). В начале процесса расширения при РКР<Р<РО относительное возрастание скорости больше относительного возрастания объёма (функция c=F(Р) более пологая, чем – v=F(Р), площадь сечения соплового канала уменьшается. При давлениях ниже критического Р<РКР, наоборот, больше относительный рост объёма по сравнению с относительным возрастанием скорости (функция v=F(Р) более пологая, чем – c=F(Р)) и площадь сечения канала увеличивается. При давлении Р=РКР скорость истечения равна скорости звука, здесь канал имеет минимальное сечение. Таким образом, только при наличии расширяющейся части в сопловом канале можно получить понижение давления ниже критического, а скорость истечения больше скорости звука. При Р=0 удельный объем газа стремится к бесконечности (v=∞), скорость истечения достигает максимального конечного значения сMAX (см. уравн. 4.9), а площадь поперечного сечения сопла (f=Gv/cMAX) стремиться к бесконечности.
В результате проведенного анализа адиабатного процесса истечения идеального газа можно сделать выводы о выборе профиля соплового канала:
если e>eКР (Р1>РКР) – сопло должно быть суживающимся, истечение газа докритическое (скорость газа на выходе из сопла меньше скорости звука);
если e<eКР (Р1<РКР) – сопло должно быть комбинированным (сопло Лаваля) с расширяющейся частью, истечение газа сверхкритическое (скорость газа на выходе из сопла больше скорости звука).
При существующем сопловом канале, если сопло суживающееся:
при e>eКР – истечение докритическое;
при e<eКР – истечение критическое, расширение газа в сопловом канале идёт только до критического давления (Р=РКР), дальнейшее расширение газа от РКР до давления за соплом Р1 идёт за пределами выходного сечения соплового канала (рис.4.4 процесс 12).
Важно отметить, что для суживающегося или комбинированного сопла, при давлении за ним ниже критического (e<eКР), в самом узком сечении сопла устанавливаются критические параметры, и дальнейшее понижение давления за соплом при постоянных начальных параметрах РО=const и ТО=const не влияет на массовый расход газа. При этих условиях расход газа через сопло ограничивается пропускной способностью его самого узкого сечения (рис.4.4 процессы 12 и 1*2*):
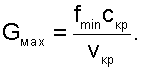 |
(4.18) |
Увеличить расход газа через сопло можно только за счёт увеличения минимального сечения сопла, в этом случае критическая скорость и удельный объем в минимальном сечении останутся неизменными, или за счёт повышения давления газа перед соплом, в этом случае критическая скорость может остаться прежней, для идеального газа:
|
|
|
|
Зависимость расхода газа от давления перед сопловым каналом при неизменном значении температуры на входе в сопло показана на рис. 4.5.
| предыдущий параграф | содержание | следующий параграф |