
Рассмотрим частные случаи политропных процессов, имеющих наибольшее распространение в практике. К таким процессам относятся: изобарный, изохорный, изотермический и адиабатный процессы. Для каждого из этих процессов оределим характеристики политропы:
n- показатель политропы,
 |
 |
 |
Изобарный процесс, протекает при постоянном давлении. Уравнение изобарного процесса Р=const.
В соответствии с уравнением политропы Pvn=const, политропа превращается в изобару Р=const при показателе политропы n=0.
Теплоемкость изобары cР при n=0 соответствует выражению c=cVk=cP.
Доля теплоты, идущая на увеличение внутренней энергии в изобарном процессе, соответствует величине α=1/к.
Кроме уравнения Р=const, для изобарного процесса можно записать уравнение 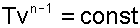 , которое при n=0 превращается в уравнение T/v=const. Таким образом, основные величины, характеризующие изобарный процесс, будут представлены выражениями:
, которое при n=0 превращается в уравнение T/v=const. Таким образом, основные величины, характеризующие изобарный процесс, будут представлены выражениями:
 |
Теплота изобарного процесса соответствует выражению:
(5.17) |
 |
(5.18) |
Изменение внутенней энергии, энтальпии и энтропии в изобарном процессе соответствует выражениям:
(5.19) |
(5.20) |
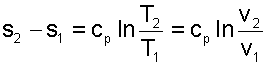 |
(5.21) |
Изохорный процесс, протекает при постоянном объеме. Уравнение изохоного процесса v=const.
В соответствии с уравнением политропы , политропа превращается в изохору v=const при показателе политропы n=±∞.
Теплоемкость изохоры при n=±∞ соответствует выражению c=cV. Доля теплоты, идущая на увеличение внутренней энергии в изохорном процессе, соответствует величине α= 1.
Кроме уравнения v=const, для изохорного процесса можно записать уравнение  , которое при n=±∞ превращается в уравнение T/P=const.
, которое при n=±∞ превращается в уравнение T/P=const.
Таким образом, основные величины, характеризующие изохорный процесс будут представлены выражениями:
 |
Теплота изохорного процесса соответствует выражению
(5.22) |
а работа изменения объема равна нулю, т.к. dv=0:
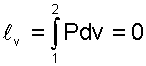 |
(5.23) |
Изменение внутенней энергии, энтальпии и энтропии в изохорном процессе соответствует выражениям:
(5.24) |
(5.25) |
 |
(5.26) |
Изотермический процесс протекает при постоянной температуре. Уравнение изотермического процесса T=const.
В соответствии с уравнением политропы Tvn-1=const, политропа превращается в изотерму Т=const при показателе политропы n=1.
Теплоемкость изотермы при n=1 равна бесконечности cт=±∞. Доля теплоты, идущая на увеличение внутренней энергии в изотермическом процессе равна нулю α= 0.
Кроме уравнения Т=const, для изотемического процесса можно записать уравнение Pvn = const, которое при n=1 превращается в уравнение Pv=const.
Таким образом, основные величины, характеризующие изотермический процесс будут представлены выражениями:
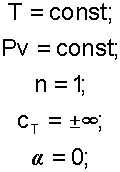 |
Теплота изотермического процесса равна работе, т.к. изменение внутренней энергии идеального газа при Т=const равно нулю.
(5.27) |
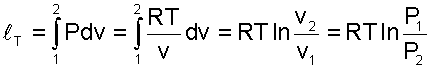 |
(5.28) |
Изменение внутенней энергии и энтальпии в изотермическом процессе для идеального газа равно нулю;
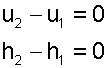 |
 |
(5.29) |
Адиабатный процесс - это процесс без теплообмена с окружающей средой, т.е. для него δq = 0 или q = 0.
Уравнение адиабатного процесса соответствует выражению s=const, т.к. δq=Tds=0 при ds=0.
Поэтому адиабатный процесс имеет еще одно название - изоэнтропный процесс.
Теплоемкость адиабаты равна нулю сs=0, т.к. температура в этом процессе изменяется, а δq=cdT=0.
Показатель политропы при сS=0 будет соответствовать выражению n=cP/cV=к, т.е. показатель политропы в адиабатном процессе равен коэффициенту Пуассона.
Доля теплоты, идущая на увеличение внутренней энергии в адиабатном процессе равна бесконечности α=∞.
Таким образом, основные величины, характеризующие адиабатный процесс будут представлены выражениями:
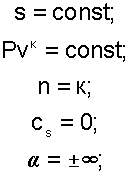 |
Теплота адиабатного процесса равна нулю, следовательно, для идеального газа в адиабатном процессе работа равна изменению внутренней энергии, взятой с обратным знаком:
(5.30) |
Изменение энтальпии в адиабатном процессе ведется традиционно h2-h1=cP(T2-T1), а изменения энтропии в этом процессе равно нулю s2-s1=0.
| предыдущий параграф | содержание | следующий параграф |